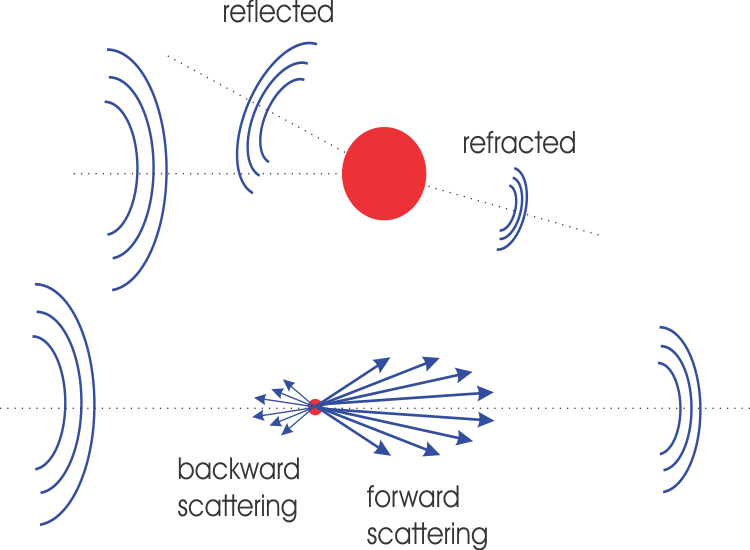
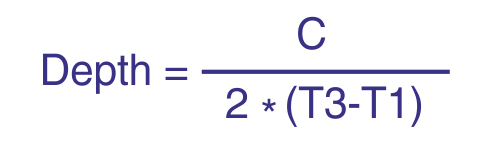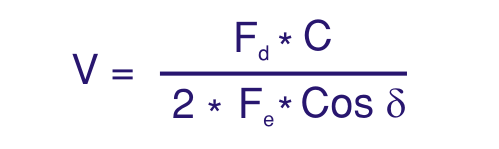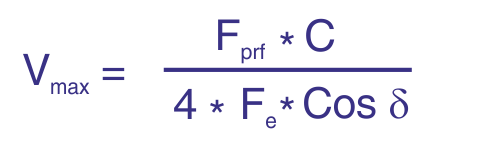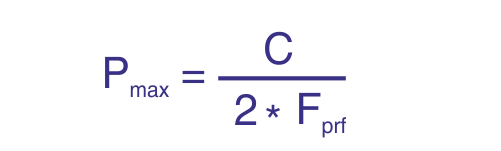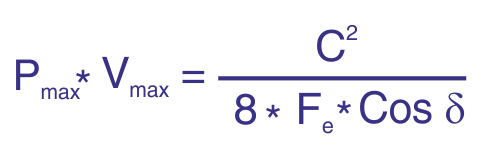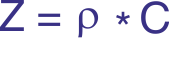Principe de fonctionnement de la vélocimétrie Doppler ultrasonore (UDV) et mesure des profils de vitesse

Technique Doppler ultrasonore

La technique Doppler ultrasonore a été initialement appliquée dans le domaine médical et remonte à plus de 30 ans. L’utilisation d’émissions pulsées a étendu cette technique à d’autres domaines et ouvert la voie à de nouvelles méthodes de mesure en mécanique des fluides.

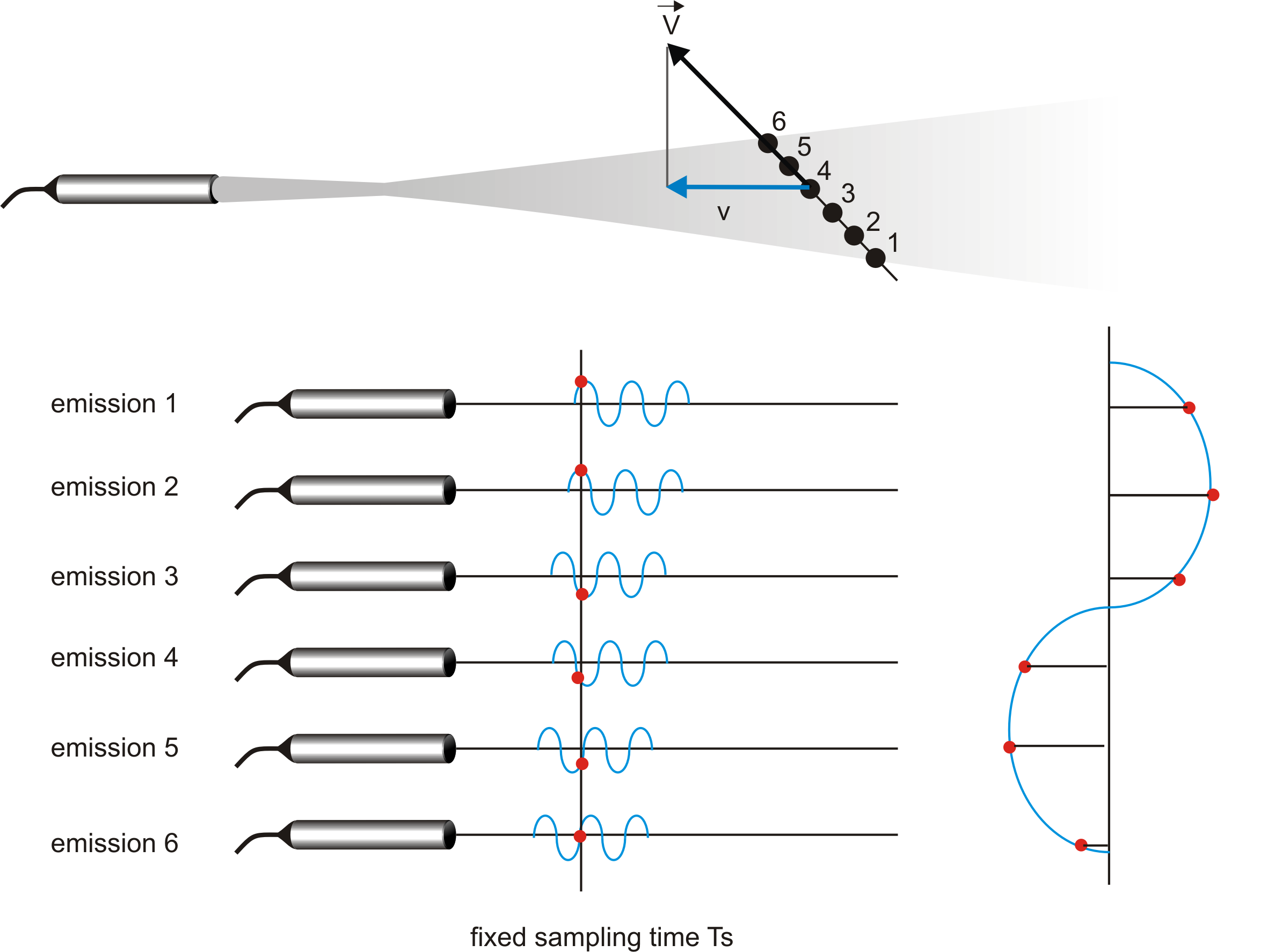
Le terme « vélocimétrie Doppler ultrasonore » implique que la vitesse est mesurée en détectant la fréquence Doppler dans le signal reçu, de manière similaire à la vélocimétrie Doppler laser. En vélocimétrie ultrasonore pulsée, toutefois, les vitesses sont calculées à partir des déplacements des particules entre impulsions successives, et l’effet Doppler ne joue qu’un rôle secondaire. De nombreuses publications, même récentes, ne font pas cette distinction, ce qui conduit à des descriptions incorrectes des systèmes et à des interprétations erronées de certains effets physiques.

Animation montrant la détection d’échos ultrasonores dans un liquide

La méthode Doppler pulsée

Au lieu d’émettre des ondes ultrasonores continues, un système Doppler pulsé envoie périodiquement de brèves impulsions ultrasonores, tandis qu’un récepteur collecte en continu les échos provenant des particules situées sur le trajet du faisceau ultrasonore. En échantillonnant les échos à des instants fixes après chaque émission, il est possible de calculer la vitesse des particules.

Comment la vitesse est mesurée

Considérons une seule particule située le long du faisceau ultrasonore. À l’instant T1, une impulsion est émise et se propage dans le liquide. À l’instant T2, l’impulsion atteint la particule. Si celle-ci est beaucoup plus petite que la longueur d’onde, elle génère un faible écho diffusé vers le transducteur, tandis que la majeure partie de l’énergie poursuit sa propagation vers l’avant.

À l’instant T3, l’écho revient au transducteur. La profondeur de la particule peut être calculée à partir du temps de parcours (T3-T1) :

Équation de la profondeur de la particule basée sur le temps de vol ultrasonore

où C est la vitesse du son dans le liquide.

Les impulsions sont émises périodiquement. Pour chaque émission, l’écho est échantillonné après un délai fixe, ce qui définit la profondeur de mesure. Si la particule se déplace entre deux émissions successives, les valeurs du signal échantillonné évoluent dans le temps et peuvent former un signal sinusoïdal.

Émissions ultrasonores multiples montrant le mouvement des particules dans le temps

Illustration de multiples particules dans le faisceau ultrasonore

L’équation principale

La fréquence du signal sinusoïdal, Fd, appelée fréquence Doppler, est directement liée à la vitesse de la particule par l’équation Doppler.

Équation Doppler reliant la vitesse de la particule au décalage fréquentiel

En pratique, de nombreuses particules sont distribuées aléatoirement dans le faisceau. Leurs échos se combinent en un signal aléatoire, mais les corrélations entre émissions successives permettent aux algorithmes d’extraire l’information de vitesse.

Avantages et limitations

Les ultrasons Doppler pulsés permettent d’obtenir instantanément des profils de vitesse complets. Cependant, comme les mesures sont réalisées périodiquement, le théorème de Nyquist limite la vitesse maximale mesurable (Vmax) pour chaque fréquence de répétition d’impulsion (Fprf) :

Équation de la vitesse maximale basée sur le théorème de Nyquist

La profondeur maximale mesurable (Pmax) est également limitée par la fréquence de répétition des impulsions :

Équation de la profondeur maximale basée sur la fréquence de répétition d’impulsion

Par conséquent, le produit de Pmax et Vmax est constant :

Produit constant entre profondeur maximale et vitesse maximale

Illustration de la relation entre Pmax et Vmax

Diffusion des ultrasons sur des particules dans un fluide

Diffusion ultrasonore

Les ondes ultrasonores se propagent dans un cône étroit et interagissent avec des particules ayant différentes impédances acoustiques. L’impédance est définie comme le produit de la masse volumique de la particule par la vitesse du son :

Les particules plus petites que la longueur d’onde produisent une diffusion arrière et ne renvoient qu’une faible partie de l’énergie vers le transducteur. Les particules plus grandes réfléchissent et réfractent les ondes, modifiant leur direction et leur intensité. La vélocimétrie Doppler pulsée repose sur des particules plus petites que la longueur d’onde afin d’éviter toute perturbation significative du faisceau ultrasonore.

Technique